El objeto más básico en Matlab es una matriz numérica con la posibilidad de almacenar números complejos. Por supuesto, los datos obtenidos en el estudio de señales y sistemas son muy bien representados en forma de matrices. En este post usaremos Matlab para la generación de señales elementales: cuadrada, triangular, entre otras.
El ToolBox de procesamiento de señales de Matlab posee una gran variedad de funciones para la generación de señales, estas señales requieren de una representación vectorial de la variable tiempo, de manera continua o discreta. Para realizar una simulación de un intervalo continuo, se usa un vector de valores discretos con un intervalo de muestreo muy pequeño.
Como vimos en
post anteriores, el siguiente comando genera un vector llamado t de valores que representan la variable tiempo, con un intervalo de muestreo de 1 ms entre 0 y 1 segundo.
t = 0:0.001:1;
Después de creado el vector que representa la variable tiempo, es posible iniciar el desarrollo de alguna señal de interés.
En Matlab una señal discreta en el tiempo se representa exactamente, porque los valores de la señal son representados como los elementos de un vector. Sin embargo las señales de tiempo continuo en Matlab son tan solo aproximaciones. La aproximación consiste de un vector cuyos elementos son muestras de la verdadera señal de tiempo continuo. Cuando se usa esta técnica para la representación de señales continuas es importante escoger el intervalo de muestreo lo suficientemente pequeño para asegurar que las muestras capturan todos los detalles de la señal.
EJEMPLOS DE SEÑALES EN MATLAB
La generación de señales periódicas tales como ondas cuadradas y triangulares es una actividad muy fácil de realizar en MATLAB.
1) SEÑAL CUADRADA
Consideremos primero la generación de una onda cuadrada de amplitud A, frecuencia fundamental w (medida en radianes por segundo) y ciclo útil rho. Recordemos que el ciclo útil es la fracción de cada periodo en donde la señal es positiva.
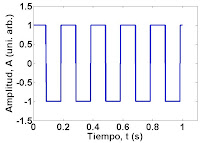
Para generar dicha señal se pueden escribir lo siguiente en la linea de comandos:
>> A = 1;
>> w = 10 * pi;
>> rho = 0.5;
>> t = 0:0.001:1;
>> sq = A*square(w*t+rho);
>> plot(t,sq);
En la segunda línea de este ejemplo, pi es una función interna de Matlab que calcula el número más cercano a la constante PI en formato de coma flotante. El último comando es usado para vizualizar la señal generada. El comando plot dibuja líneas conectando los valores sucesivos de la señal y así da la apariencia de una señal en tiempo continuo.
2) SEÑAL TRINGULAR
Consideremos ahora la generación de una onda triangular de amplitud A, frecuencia fundamental w y ancho Wdt . El periodo de la onda triangular será T con el máximo valor de la señal ocurriendo en t = WT . El comando básico para generar esta señal es:
A * sawtooth(w * t + Wdt)
El resultado se puede observar en la gráfica a la izquierda
3) SEÑAL ESCALÓN
En Matlab, el comando ones(M, N) genera una matriz de unos de tamaño MxN, y el comando zeros(M, N) es una matriz de ceros del mismo tamaño. Se puede hacer uso de estas dos matrices para generar dos señales comúnmente usadas: la señal escalón y la señal impulso.
Una señal paso de amplitud uno, puede ser generada con el siguiente comando.
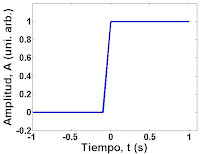
U = [zeros(1, 10), ones(1, 11)];
Para la versión continua creamos un vector que represente el tiempo el cual tenga muestras de un intervalo separados por valores muy pequeños. Los comandos y los resultados se muestran a continuación:
>> u=[zeros(1,10),ones(1,11);
>> t=-1:0.1:1;
>> plot(t,u)
Como se menciono anteriormente, una señal generada en Matlab es inherentemente de naturaleza discreta. Para visualizar una señal en tiempo discreto se puede hacer uso del comando stem. Específicamente stem(n, x), bosqueja los datos contenidos en el vector x como una señal de tiempo discreto con los valores de tiempo definidos por el vector n. Los vectores n y x deben tener dimensiones compatibles, es decir deben tener el mismo número de elementos. Así, para este caso para obtener la representación de esta señal en tiempo discreto creamos un vector-tiempo el cual debe tener valores separados por una unidad.
>> u=[zeros(1,10), ones(1,11)];
>> n=-10:10;
>> stem(n,u)
Recuerde que para poder usar las funciones plot y stem, es requisito que los vectores (t y u) ó (n y u) tengan iguales dimensiones. Por esta razón el vector u se forma como una composición de diez ceros y 11 unos, debido a que los arreglos t y n, tienen dimensión 21 dado que incluyen un elemento central el cual es el número cero. Para probar este hecho, se puede hacer uso de la función Matlab llamada size que devuelve como resultado un vector con las dimensiones de la matriz que se le pasa como parámetro.
4) SEÑAL IMPULSO:
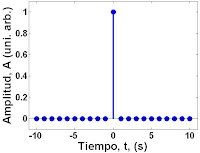
La versión discreta de la señal impulso se puede también generar con ayuda de las funciones zeros y ones, realizando una composición como sigue:
>> delta = [ zeros( 1 ,10 ), 1 , zeros( 1 ,10 ) ];
>> n = -10:10;
>> stem(n,delta);
5) SEÑAL RAMPA
Para generar la señal rampa, tan solo es necesario recordar que esta función puede ser creada, como la composición de una recta Y(x) = x a partir de cero y de la recta Y(x) = 0 para valores de x menores de cero, así la versión discreta se muestra a continuación:
>> t1=0:0.1:10;
>> rampa1=t1;
>> rampa=[zeros(1,101),rampa1];
>> t2=-10:0.1:0;
>> t=[t2,t1];
>> plot(t,rampa)
Ejercicios:
1) Desarrollar un conjunto de comandos Matlab para aproximar las siguientes señales periódicas en tiempo continuo, dibujando 5 ciclos de cada una:
a) Onda Cuadrada, de amplitud 5 Volts, frecuencia fundamental 20 Hz y ciclo útil del 60%.
b) Señal diente de sierra, amplitud 5 Volts y frecuencia fundamental 20Hz