Comparación del desempeño de un filtro convolución y un filtro pasa bajas de promedios ponderados en una misma función/señal

Ahora mostramos dos ejemplos de filtros. La funcion a trabajar es:

La cual tiene un pico extendido en t=5 y dos pequeños picos de estructura en t=2. Pues bien la entrada a un instrumento  cuenta con  filtro descrito por:

Efectivamente, la señal filtrada por  convolución será la transforma de Fourier inversa de la multiplicación de las transformadas de Fourier de la señal y del filtro; es decir:

A continuación aplicaremos el filtro en código Matlab.

Filtro 1: Convolución.

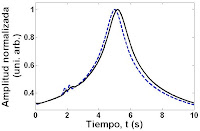
Para comparar la señal y la salida filtrada, a ambas las normalizamos. Observamos que hay un corrimiento en el tiempo. Este efecto en los indices y en la amplitud son muy comunes cuando se usa la transformada de Fourier.

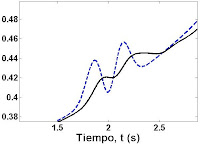
Adicionalmente, una vista cercana a la estructura de los dos picos pequeños muestra que la salida del filtro cuenta con estos picos más pequeños y casi sin desernir. Con todo, esta forma de presentar los datos muestra a detalle que el filtro es bueno sin ser excelente para eliminar la estructura de la curva principal .

A continuación, mostramos el código Matlab utilizado para hacer estas curvas.

 %%% Inicio código 1: Filtro convolución

 clc

clear

close all

x = 0:0.0001:10;

y = 4*((sin(x-2)).^2).*exp(-50*((x-2)).^2) + 0.5*( ((x-5).^2 +0.25).^(-.25) );

r = ones(size(x));

for k= 1:length(x)

    if x(k) <= 0.15

        r(k)= .50;

    elseif x(k) <= 0.30

        r(k)= 0.25;

    elseif x(k) <= 0.60

        r(k)= 0.10;

    else

        r(k)= 0;

    end

end

plot(x,r,  'LineWidth',3)

axis([-.2,3,-0.2,0.6])

Y= ifft( fft(y).*fft(r));

figure

hold on

plot(x, y/max(y), '--b','LineWidth',3)

plot(x,Y/max(Y), 'k', 'LineWidth',3)

axis([0,10,0.28,1.05])

hold off

%%% Fin código 1: Filtro convolución

Filtro 2: Pasa bajas con promedio ponderado

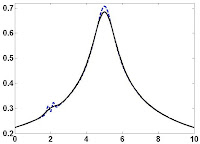
Ahora bien, utilizaremos el filtro pasa bajas (PB), que ya mostramos en otro post, en este caso usamos 6,0000 iteraciones. Dado que la estructura en la función puede representar una oscilación rápida aplicaremos el filtro PB.   Observamos en la salida que tanto el cambio en la amplitud como el corrimiento en los indices de los vectores de las curvas es casi minimo. Además de que se ve más disminuida la estructura en la función.

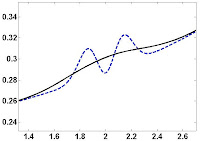
Este filtro PB presenta mejores resultados que el de convolución; esto es por el tipo de filtro r(t) utilizado. Sin embargo, el filtro PB  tarda mucho más en desarrollarse. Puedes  usar los comandos de Matlab TIC yTOC antes y despues de que inicien las rutinas para observar la velocidad de ejecución de cada función o escript.

Podemos asegurar que dependiendo que se busquemos filtrar, hay un filtro que nos funcionara mejor que otros, pero hay que saberlo encontrar :)

A continuacion el segundo código Matlab:

%%% Inicio código 2: filtro pasa bajas con promedio ponderado

clc

clear

close all

tic % inicia el contador de tiempo

t = 0:0.001:5*pi;

f = 4*((sin(t-2)).^2).*exp((-50)*(t-2).^2) +0.5*((t-5).^2+0.25).^(-0.25); %señal de trabajo

hold on

plot(t, f, 'r') % para visualizar la señal con ruido

for corrida = 1:60000 %iteracion del filtro

for k = 2:(length(t)) -1 ;

f(k) = 0.25*(f(k-1) + 2*f(k) + f(k+1)); %filtro

end

end

plot(t, f, '--b') %para visualizar la señal filtrada

hold off

toc %finaliza el contador del tiempo

%%% Fin código 2: filtro pasa bajas con promedio ponderado

Ejercicios: 

1) Muestre el grado de atenuación de las protuberancias después de pasar por el filtro.

2) Diseñe otro filtro de convolución que atenue mejor a los dos picos que forman protuberancias en la curva original

3) Calcule la salida del filtro de convolución con r(w)*I(w) en lugar de  I(w)*r(w). Describa sus observaciones.